only interval that is perceived as being the same as the note above or below it.
You need only go to a keyboard, play (and hold) any 'A' and the 'A' above and/or below it
to notice that it sounds like the same note. You can also listen to the "Sound of Music"'s
Do-Re-Mi song to get the feeling that the 'Ti' "That will bring us back to Do" really is
a return to the 'Do' the song started on.
You might also think of male and female voices singing the same melody from a single staff
of notation. There's a distance between the male and female voices but somehow it sounds like
a single note . . . only richer because of the octave difference between the lower and higher
male and female voices. It's also possible for the female alto and soprano voices to sing an
octave apart with the male tenor and bass voices singing an octave apart so that you have four
occurances of the note and it will still sound as if there were only one very full sounding note.
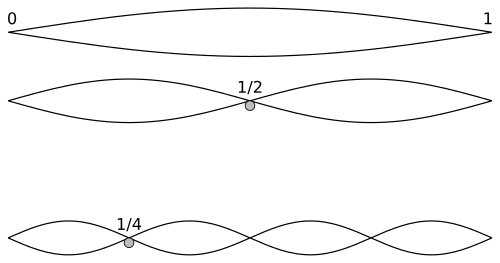
The interval of an octave is the first overtone in this depiction of the
overtone series of harmonic sound. You can see that there are two crests of the
overtone for the one crest of the fundamental, with each crest half the length of the fundamental's.
You find that same relationship again between the 1st and 3rd overtones (1/2 and 1/4)
since there are again two crests for each of the two crests of the overtone below it.
Visually, there is the relationship of 2 to 1 between the first overtone and the
fundamental, and then again between the 3rd and 1st overtone. If the image showed
the next overtone corresponding to an octave you'd see the same 2 to 1 relationship
between the 7th and 3rd overtones (1/8 to 1/4).
Also, if this image included subharmonics, the first subharmonic would show one
crest peak (but not the return) for the one cycle of the fundamental. The
terminology of fundamental, overtones, partials and harmonics can get confusing.
And it doesn't help that sometimes the starting point (what I'm calling the fundamental)
is sometimes called the first harmonic and the rest numbered 2,3,4,.. while at other times
the fundamental is treated as zero and its overtones numbered 1,2,3,..
Both zero and one make sense for the fundmental if we turn to mathematical notation.
Any number raised to the zeroth power is the number 1. Combine that with the knowledge
of the interval of an octave being
twice the note below it (or half the note above it)
and we can express the series of harmonics (and subharmonics)
that are octaves as "powers of 2".
More familiarly, the "powers of 2" are [.., 1/8, 1/4, 1/2, 1, 2, 4, 8, ..]
If we take the note 'A' in the middle of a keyboard, we could express the octaves above and below A-0 like this:
A-0, like 2 to the zeroth power, is not "zero" in the sense of an absence of sound or quantity.
It's "Ground Zero" as in a point of origin.
In music, the octave is perceived as a return to the starting point.
In number systems, the "number being raised to powers" is the base of that number system.
If we're counting upwards from '1' (base of number system to the zeroth power),
then every time we reach the next highest "power of the base" . . . it is a return to the base of the system.
We're most familiar with the decimal or "base 10" system. Our digits go from 1-9 with zero
functioning as a place holder when we get to the next occurrence of the base.
What for us is: 10, 100, 1000 ... was for the Romans: X, C, and M respectively. The 1-9 notation
in a base 10 system makes it much, much easier to do calculations. but the underlying
counting numbers are the same regardless of how they're spelled out. Like music, mathematics
developed in all civilizations and all of them followed the same rationale and
organizational principles. The mathematics of today and the musics of today have grown
in ways peoples of 2,000 years ago would never have imagined, though the
foundational principles they established remain unchanged. This should not be surprising if
we were to consider that math and music are rational and visceral outgrowths of the
same exact phenomenon of the octave within the overtone series of harmonic sound.