Natural Order of Harmonic Sound

Prayer of Perichoresis - home

Perfectible Harmony - home

Somewhere in the nineteenth century, mathematicians found that any complex sound
could be disassembled into a series of simple sine waves that when added together
would result in the original complex sound. The pitch at which we hear the complex
is called the fundamental since starting point or base to which the other sine waves are
added. The other sine waves are called overtones or harmonics. The collection of all the
various sine waves starting with the fundamental is called the harmonic or overtone series.

Overtones can ccur anywhere on the continuum of sound. They don't change the
pitch of the fundamental but add color and character which in some instances we perceive
as quality; in other instances as conveying information; but always as a means of
distinguishing and identifying the sound's source. The sound of the wind or the ocean
or a specific animal or Bob . . . or a cello, alto sax or glockenspeil.

When it comes to musical instruments the overtones no longer occur "just anywhere"
above the fundamental. They very specifically occur at 2x's, 3x's. 4x's, etc. the
pitch of the fundamental. We're not consciously aware that the overtones are integer
multiples of the fundamental, but we very definitely perceive the complex sound as
having the quality of purity.

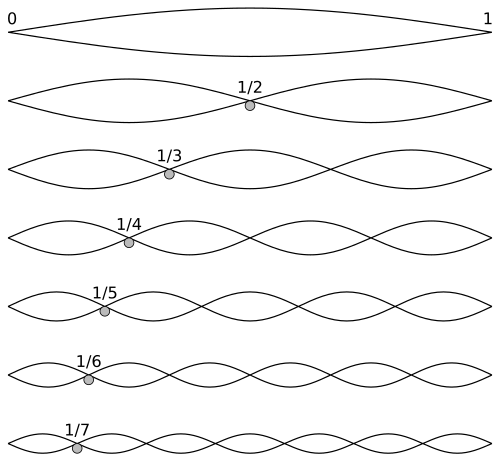I grabbed this image of a vibrating string from Wikipedia's page
"Harmonic Series (music)" thinking it's public domain. If it's not,
please let me know and I'll make an effort to replace it with a
similar image that is.

In any event, what you can see in the image is that there are two crests, then
three,four,five,.. crests of each overtone for the one crest of the fundamental.
Each overtone is vibrating 2,3,4,5 times as fast as the fundamental, but their
cycles all align with the start and end point of a single cycle of the fundamental.

This alignment gives an easy explanation of why we consider tones whose overtones
are only integer multiples of the fundamental as being pure, but I don't know if that's
actually true. Since the overtones of musical instruments have been found to adhere
to this particular ordering of the overtones however, there's no debating this simple
fact of nature and no end to wondering why pure tones elicit a strong enough guttural
in humans to warrant their spending time crafting and playing flutes as early as 50,000 BC!

So far, we're only talking about the quality of an individual tone at a particular frequency
that does not move from that frequency over time. But we don't generally listen to a single
unchanging tone for extended periods of time. Nor do we listen to tones sliding around willy-nilly.
What we listen to are melodies. Tones that move by discrete amounts. And melodies don't just
wander all over the place. They resolve to a satisfying and logical place of rest. It's not a
logic to grasp with our capacity for reason, but a visceral logic. Growing out of our perception
of overtones that are integer multiples of the fundamental producing the purest individual tones,
neighboring tones that are separated by ratios corresponding to the integers separating the
overtones are perceived as the ideal spacing between them.

The Thing is: the only thing that makes overtones occurring at exactly [2,3,4,5,..] times the funadamental special is that that precise ordering evokes a limbic state that
only human beings perceive as good and desireable for the sake of its beauty. I'm even going to go so far as to say a love for the beauty. Why else would certain primitive
humanoids have taken time away from surviving and procreating to begin crafting flutes? And not just in one place, but several distant and concurrent places. A more
interesting question is how/why all primitive humanoids the world over evolved cerebral and muscular capacities that single out this unique ordering of the fundamental
and overtones? It couldn't have been just one person who "fell for" the perceived beauty and told two people who told two people . . . with the result that eveyone agreed
with the exact same proportions of pure and perfect musical intervals.

Humans were vocalizing well before a few of them starting crafting instruments that built upon "the ordering principle" they already knew from their own vocal chords
and the aural areas of the cerebral cortex. There are other ordering principles such as the Fibonacci sequence that recur throughout nature, and while we do recognize the
beauty of the series in biological arrangements of leaves and shells, no other ordering principle captivated and influenced humanity and strongly as the harmonic series.

That may sound like a bold statement making music a bigger deal than it really is, but think about this: If humans evolved the capacities to perceive, produce and desire
sounds adhering to the integer order of harmonic sound, then long, long, long before mathematics came about, humans were limbic-ally and viscerally familiar with what
would tens and possibly hundreds of thousnads of years later be known as the natural numbers - excluding zero: [1,2,3,4,..].

If you're willing to explore the phenomenon of the musical interval called the octave, then I can weave a tale of how not only were counting numbers embedded in our pysche,
but the entire ediface of a mathematical system of logical and reliable interrelations. After all, since the octaves are represented by [1,2,4,8,..] -- when that set is interspersed
with the remainng intergers [3,5,6,7,9,10,..] -- what you end up with is the binary number system! From that perspective, it's hard not to see the origins of math as well as the
origins of music in order of harmonic sound.

NOTICE: This website does not use cookies. I couldn't care less about any of your personal information.
If anyone does email me I'll reply if it seems a reply is in order, but I'm not going to put an email list together or engage in any kind of general mailing.